The Lambda Calculus¶
A Quote to Start the Day¶
You realize that everything can be done with function composition?… It’s called lambda calculus.
—Joseph McKinsey
The Lambda Calculus¶
The \(λ\)-calculus is a mathematical language of lambda terms bound by a set of transformation rules. The \(λ\)-calculus notation was introduced in the 1930s by Alonzo Church.
Just like programming languages, the \(λ\)-calculus has rules for what is a valid syntax:
| Variables: | A variable (such as \(x\)) is valid term in the \(λ\)-calculus. |
|---|---|
| Abstractions: | If \(t\) is a term and \(x\) is a variable, then the term \(λx.t\) is a lambda abstraction. |
| Applications: | If \(t\) and \(s\) are terms, then \(ts\) is the application term of \(t\) onto \(s\). |
Anonymous Functions¶
Lambda abstractions can be thought of as anonymous functions in the \(λ\)-calculus.
A lambda abstraction which takes an \(x\) and returns a \(t\) is written as so:
Example
Suppose in mathematics we define a function \(f(x) = x + 2\). This could be written as \((λ x.x + 2)\) in the \(λ\)-calculus [1]. Of course, this function is anonymous and not bound to the name \(f\).
| [1] | Of course, we haven’t said that either \(+\) nor \(2\) is valid in lambda calculus yet. We will get to that… |
Functions are First Class¶
In the \(λ\)-calculus, abstractions are not only first class functions, they are our only way of to encode data.
Abstractions are used to encode everything:
- Numbers
- Booleans (true/false)
- Conses
- …
Currying¶
Since abstractions in the \(λ\)-calculus may only take one argument, currying is typically used to denote functions of multiple arguments. For example, the function \(f(x, y) = x\) might be written as:
Further, function application is left-associative, so \(fxy\) means \((fx)y\).
Free and Bound Variables¶
The \(λ\) operator (which creates lambda abstractions) binds a variable to wherever it occurs in the expression.
- Variables which are bound in an expression are called bound variables
- Variables which are not bound in an expression are called free variables
Example
With your learning group, identify the free and bound variables in this expression:
Transformations¶
| \(\alpha\)-conversion: | |
|---|---|
| Allows variables to be renamed to non-colliding names. For example, \(λx.x\) is \(\alpha\)-equivalent to \(λy.y\). | |
| \(\beta\)-reduction: | |
| Allows functions to be applied. For example, \((λx.λy.x)(λx.x)\) is \(\beta\)-equivalent to \(λy.(λx.x)\). | |
| \(\eta\)-conversion: | |
| Allows functions with the same external properties to be substituted. For example, \((λx.(fx))\) is \(\eta\)-equivalent to \(f\) if \(x\) is not a free variable in \(f\). | |
Examples: Alpha Equivalence¶
With your learning group, identify if each of the following are a valid \(\alpha\)-conversion. Turn in your answers on a sheet of paper with all of your names at the end of class for learning group participation credit for today.
- \(λx.λx.x \to λy.λy.y\)
- \(λx.λx.x \to λy.λx.x\)
- \(λx.λx.x \to λy.λx.y\)
- \(λx.λy.x \to λy.λy.y\)
Examples: Beta Reductions¶
Fully \(\beta\)-reduce each of the following expressions:
- \((λx.λy.λf.fxy)(λx.λy.y)(λx.λy.x)(λx.λy.y)\)
- \((λa.λb.a(λb.λf.λx.f(bfx))b)(λf.λx.fx)(λf.λx.f(fx))\)
Church Numerals¶
Since all data in the \(λ\)-calculus must be a function, we use a clever convention of functions (called Church numerals) to define numbers:
| 0: | \(λf.λx.x\) |
|---|---|
| 1: | \(λf.λx.fx\) |
| 2: | \(λf.λx.f(fx)\) |
| 3: | \(λf.λx.f(f(fx))\) |
… and so on. In fact, the successor to any number \(n\) can be written as:
Notice this
Defining numbers as functions in this way allows us to apply a Chuch numeral \(n\) to a function to get a new function that applies the original function \(n\) times.
Shorthand Notations¶
While it’s not a defined part of the \(λ\)-calculus, we define common shorthands for some features:
- \(0, 1, 2, \ldots\) are shorthand for their corresponding Church numerals
- \(\{\text{SUCC}\} = λn.λf.λx.f(nfx)\)
Note
The notation “\(=\)” above is not a part of the \(λ\)-calculus. I’m using it for saying “is shorthand for”.
Addition and Multiplication¶
Adding \(m\) to \(n\) can be thought of as taking the successor to \(n\), \(m\) times. Using our shorthand \(\text{SUCC}\), this can be written as:
Similarly, multiplying \(m\) by \(n\) can be thought of as repeating \(\text{ADD}\, n\), \(m\) times and then applying it to \(0\), this can be written as:
Boolean Logic¶
We use the following convention for true and false:
From here, we can define some common boolean operators:
Cons Cells¶
By convention, we will represent a cons cell as a function that applies its argument to the CAR and CDR of the cons cell. This leads to the shorthand:
Using this, we can define lists:
What else is there in Lambda Calculus?¶
- Getting the predecessor (
{PRD}) for a Church Numeral is hard, but doable (extra credit). To subtract \(m\) from \(n\), apply the{PRD}function \(m\) times to \(n\). - For recursion, we need to reference ourselves in a lambda abstraction. This is done using a Y-combinator.
- The graduate level Theory of Computation (CSCI 561) class talks much more extensively about the \(λ\)-calculus.
- There are many extensions to the \(λ\)-calculus such as those encoded by the \(λ\)-cube.
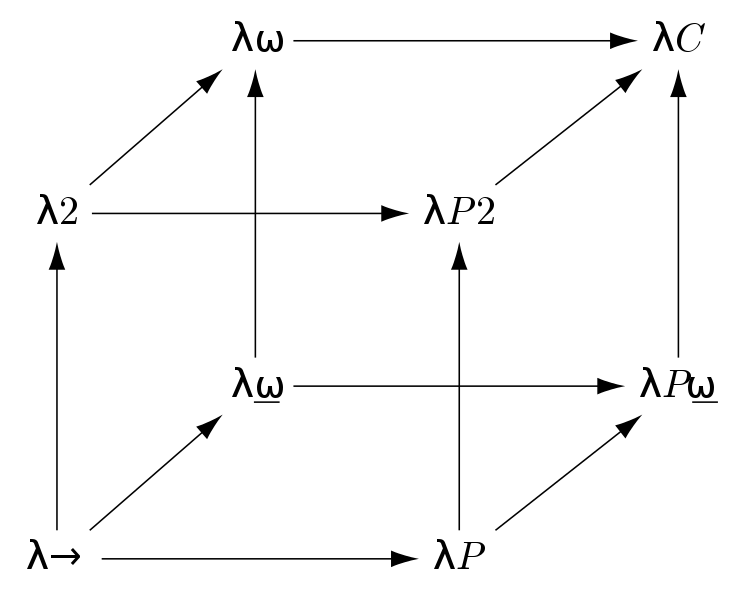
Why is any of this Useful?¶
- \(λ\)-calculus can emulate a Turing machine. That means that anything you can do with a classical computer, you can do with the \(λ\)-calculus. This fact underpins all of functional programming.
- Many functional programming languages (e.g., Haskell, Scheme, SlytherLisp) are just practical implementations of the \(λ\)-calculus.
- The \(λ\)-calculus gives us another perspective on type theory (using the generalization of the \(λ\)-calculus called typed \(λ\)-calculus).
- It is another way for us to quantify what is computable.