Posted
on
in
Matrix, Programming
• 2755 words
• 13 minute read
Tags:
Cryptography, E2EE, Megolm, Encryption, Integrity, Verification, Ratchet
In Matrix, message security is provided by Megolm. The goal of message security is twofold. We (a) want messages to be encrypted on the sender’s device and (b) only be able to be decrypted on devices of users who are a part of the conversation. As a corollary, we want to prevent other parties (rogue homeservers, man-in-the-middle attackers, etc.) from decrypting the messages.
In this article I describe Megolm1, and explain what security guarantees it provides and how it provides them. I will be focusing on Megolm itself, rather than on Olm as there are already many resources for learning about Olm (the Signal Double-Ratchet Algorithm).
This article requires some basic understanding of the following cryptography concepts:
- Encryption (symmetric and asymmetric)
- Asymmetric signatures
- Hashes and HMAC
- Key-Derivation Functions (HKDF)
If you are unfamiliar with any of these topics, check out the Matrix Cryptography Prerequisites companion article which describes the prerequisites in enough detail to understand the rest of this article.
The following figure describes the mechanism by which Megolm provides message security. There’s a lot here so don’t worry, I will go through each piece individually and by the end of this article, you will understand all of the pieces of this figure.
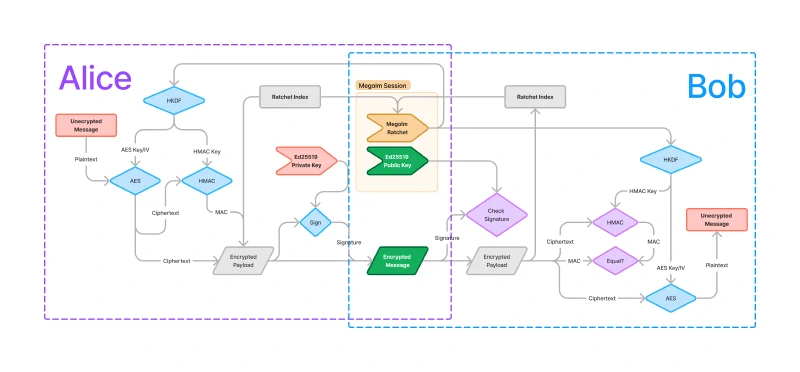
The red nodes represent data that does not leave the corresponding user’s device, green nodes represent data that can be published anywhere, and orange nodes represent data that can be shared, but only with users Alice wants to be able to read the messages. The blue nodes represent cryptographic operations that are required for encryption and decryption while the purple nodes represent cryptographic operations that are used to verify data integrity, but are not necessary for the decryption flow. The grey nodes represent intermediate values.
Note that “Alice” and “Bob” are just convenient names for the sender and receiver devices. The process is the same for devices belonging to the same user, and even your own device when you re-decrypt your own messages.
I will start by orienting us in section 1. Overview and then discuss the three main security features that Megolm provides in sections 2. Message Encryption, 3. Message Integrity, and 4. Origin Verification. I will then briefly discuss how Megolm sessions are shared between devices in section 5. Sharing the Megolm Session and then in section 6. What is a Megolm Ratchet Anyway? I describe the ratchet mechanism at a high level. I make a few concluding remarks in section 7. Conclusion.
1. Overview
Let us start by making a few observations about the overall dataflow in Figure 1.
Notice that the unencrypted message is on both Alice’s and Bob’s side, but the unencrypted message itself never leaves Alice’s device. Instead, the plaintext message undergoes a series of transformations to end up in an encrypted message and then back from that encrypted message to the plaintext.
In the overlapping section between Alice and Bob, there are two pieces of data:
the encrypted message and the Megolm Session. Alice’s and Bob’s devices share
the encrypted message via an m.room.encrypted Matrix event within a Matrix
room. The Megolm session must also be shared as it contains information about
how to encrypt and decrypt messages. I will discuss the mechanisms by which the
sessions are shared in section
5. Sharing the Megolm Session.
If you look at both Alice’s and Bob’s side of the diagram, you’ll notice that there are many similarities. Both sides pull data from the ratchet and apply HKDF to expand the key into an AES key and IV as well as an HMAC key. Both sides use AES to (en/de)crypt the message, and HMAC to generate a MAC. This is natural because Bob’s side needs to “undo” the encryption applied by Alice’s side.
In the next three sections I will break down the dataflow by looking at which pieces of the dataflow are required for encryption, message integrity, and origin verification.
2. Message Encryption
Message encryption prevents attackers from reading the contents of the message without having the proper key. The highlighted parts of the diagram below represent the components of Megolm which provide message encryption.
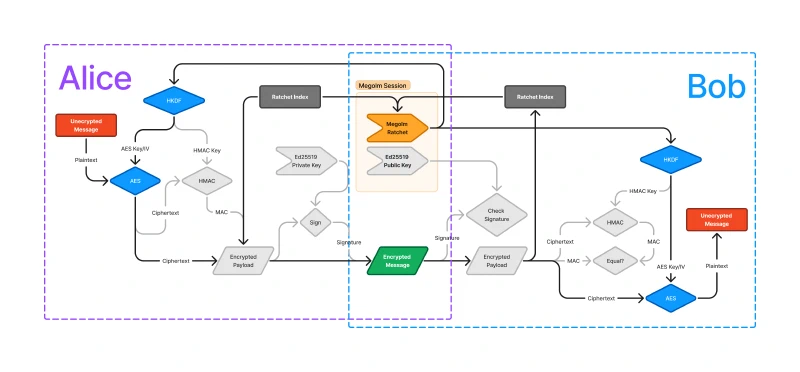
Encryption is provided by AES with a key and IV derived using HKDF from the Megolm ratchet.
On both ends of the diagram, the unencrypted message is encrypted or decrypted using AES (symmetric encryption). AES itself is quantum-resistant, so even if an attacker with a powerful quantum computer gets a hold of the encrypted messages within a room, they will not be able to easily decrypt the messages.
Matrix uses AES-256-CBC2 which requires a 32-byte key and a 16-byte IV, so the natural question is: where do we get the key and IV from?
A simple (albeit very impractical) method that would provide equivalent security to what Matrix provides would be for Alice and Bob to convene in-person before every message and exchange the AES key and IV for that message. Obviously this is impractical. Instead, Megolm relies on the shared Megolm ratchet to produce keys. I will discuss the mechanics of the Megolm ratchet in section 6. What is a Megolm Ratchet Anyway?, but right now, it is sufficient to know that the ratchet takes a ratchet index and deterministically produces a sequence of bits. The sequence is not suitable for use directly in AES, so we use HKDF to derive an AES key and IV.
Both Alice and Bob have the ratchet as part of the Megolm session, and the ratchet index is included in the encrypted message payload, so both sides of the conversation are able to use the ratchet to produce the same value. Both sides also use HKDF (which is also deterministic) to generate the same AES key and IV.
Multiple messages can be sent using the same Megolm session. The ratchet index should be incremented for each new message.
3. Message Integrity
Now, let’s consider the situation where an attacker is able to modify the contents of the message in transit. How can we detect if this happens? This is where the concept of message integrity comes into play.
Ensuring message integrity requires guaranteeing that the contents of the message have not been tampered with. We want to know if an attacker has edited the encrypted message. The highlighted parts of the diagram below represent the components of Megolm which guarantee message integrity.
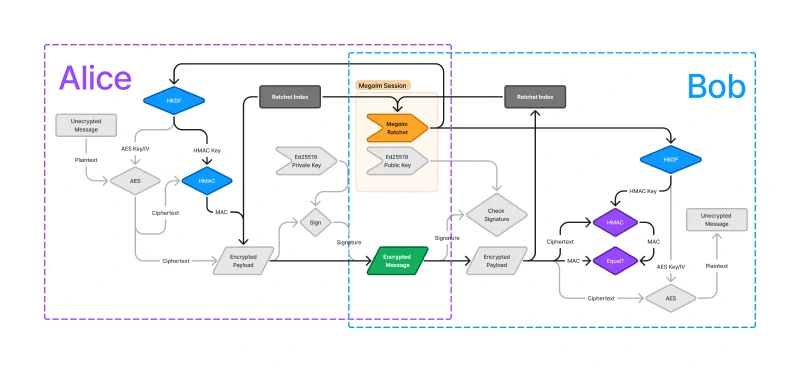
Message integrity is provided by HMAC with a key from the same HKDF output as the AES key and IV.
After computing the ciphertext by running AES, a MAC is created using HMAC using the ciphertext and an HMAC key derived from the same HKDF output as the AES key and IV. HMAC requires a hash function, and Matrix uses SHA-256. The MAC is used as a checksum for the message. If a single bit of either the MAC or of the ciphertext is changed, Bob will not be able to verify the MAC.
On Bob’s side, the MAC is included in the encrypted message, and Bob can use the same process (HKDF -> HMAC) to generate the same checksum as Alice did. If the MAC in the encrypted message matches the MAC that Bob computes, then he can know that the message was not modified in transit.
4. Origin Verification
Next, recall from the overview that the Megolm session is shared between all of the devices of users that are in the corresponding Matrix room. This means that anyone can use the ratchet to decrypt messages. However, all of the encryption operations in the previous two sections can be performed with only the ratchet as well.
This means that an attacker could create a message that could be decrypted using the Megolm session. To remedy this, Megolm uses an asymmetric signature to verify that the creator of the message is the same as the creator of the Megolm session. It is critical that the receiver (Bob) also verifies the signature to ensure that the message is from the creator of the Megolm session. The highlighted parts of the diagram below represent the components of Megolm which allow Bob to verify that Alice generated the message.
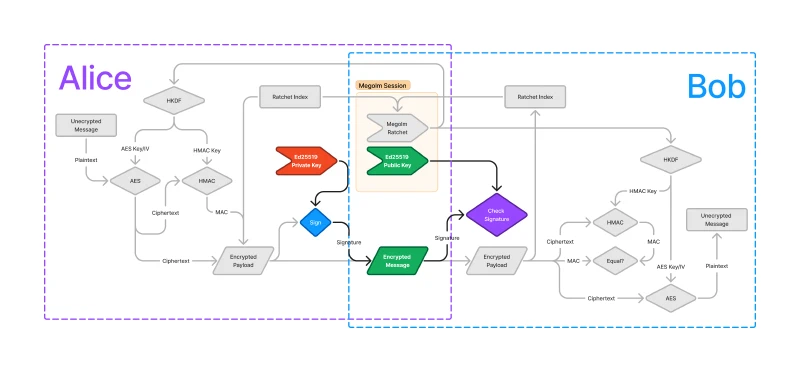
Origin verification is provided by an Ed25519 signature of the encrypted payload.
Every Megolm session has an Ed25519 private/public keypair associated with it. The public part of the key is included as part of the session, while the private part of the key is stored only in Alice’s device.
After the encrypted payload is produced from the AES ciphertext, MAC, and the ratchet index, Alice signs the entire payload using her Ed25519 private key for the Megolm session. Remember, this private key never leaves her device, so only Alice can create a valid signature. When Bob receives the message, he must first check the signature using the Ed25519 public key which is included in the Megolm session. If the signature check passes, then Bob can know that the device which has the Megolm session’s private key must have created the message.
5. Sharing the Megolm Session
So far we have looked at what security features Megolm provides and how the Megolm session is essential to providing said security. But we also need to discuss how the Megolm session is shared to other devices in the room.
There are three main ways that Megolm sessions are shared:
Olm-encrypted
m.room_keyto-device events. These are used to send the Megolm session to all of the devices in the room when the user sends their first message with a specific Megolm session.Olm-encrypted
m.forwarded_room_keyto-device events. These are used to request Megolm session keys from other devices belonging to the same user. For example, when you sign in to a new device for the first time, your client could sendm.room_key_requestevents to your previously logged in clients for the keys that it does not have. Those clients could opt to forward you the requested room key.Clients should only forward keys to verified devices of the same user.
Key Backup. This is a mechanism where the keys are encrypted with a backup key and then stored on the homeserver. Clients can restore keys from the backup using the backup key.
I’ll note here that in Matrix, Megolm sessions are sometimes referred to as “room keys”, hence the name of the to-device events.
The details of Key Backup will be discussed in my upcoming talk at the Matrix Conference which will have an accompanying blog post.
Note that the Megolm session is shared separately from the encrypted message
payload which is shared via an m.room.encrypted event. This can cause Unable
to Decrypt (UTD) errors if the Megolm session share fails but the event is sent.
6. What is a Megolm Ratchet Anyway?
So far I have discussed how Megolm provides message encryption, message integrity, and origin verification. Each of these features require some data from the Megolm session. Message encryption and integrity require the ratchet, and origin verification requires the Ed25519 public key. The Ed25519 public key is self-explanatory, but so far I’ve been very hand-wavy with what the ratchet is. In this section I will describe at a high level the functionality that the ratchet provides and how it does so. I am not going to dive into a detailed cryptographic explanation of how the ratchet works since the Megolm documentation already accomplishes that goal quite well.
The megolm ratchet behaves similarly to a mechanical odometer or one of those people counter devices that are used to count the number of people who have passed a checkpoint (see Figure 5). Every time the button is pressed, the 1s place is incremented. When the 1s place rolls over back to 0, the 10s place is incremented. The same applies to the 10s -> 100s and 100s -> 1000s place, etc.

Credit: Amazon
The Megolm ratchet also has four parts, but there are a few fundamental differences in how the people-counter ratchet and the Megolm ratchet behave:
| People Counter | Megolm | |
|---|---|---|
| Starting Point | starts at 0000 | starts with four random 256-bit values in each of the four positions for a total of 1024 bits |
| Incrementing | each position is incremented by adding 1 | each position is incremented using HMAC (the details are not important, but recall that HMAC is irreversible) |
| Rollover | when a position reaches 9, on the next increment it resets back to 0 | when a position has been incremented \(2^8-1=255\) times, on the next increment it is reset by using the next higher position’s value as the HMAC key |
| Skipping Values3 | impossible (must always increment by 1) | possible to skip by increments of \(2^0=1\), \(2^8\), \(2^{16}\), or \(2^{24}\) or any combination thereof4 |
So what does this get us? The 1024 bits of entropy that the ratchet is initialized with provides enough randomness for all of our AES key/IV and MAC key needs for the lifetime of the Megolm session. Additionally, since the ratchet parts are incremented using HMAC, we get forward secrecy. That is, if an attacker gets a hold of a ratchet value, they cannot get previous ratchet values (and thus cannot decrypt the messages encrypted with previous ratchet values).
Recall from section 2. Message Encryption that the bits produced by the ratchet are not suitable for use directly in AES? Well, now you can see the reason: significant portions of the random value are not permuted on each ratchet. Except for every 256th increment, only the last 256 bits are updated. HKDF spreads out the entropy across all of the bits of its output which is used as the AES key and IV as well as the MAC key.
7. Conclusion
Now that I’ve discussed how all of the components work, let’s walk through the process of sending and receiving a single message (assuming that Alice has already shared the session with Bob). Here’s the diagram from the start of the article:

When Alice wants to encrypt a message, she first determines the next ratchet
index. Alice uses the Megolm ratchet to generate bits and passes those bits
through HKDF to produce an AES key and IV and a MAC key. She then takes her
message, encrypts it with AES, and creates a MAC of the ciphertext using the MAC
key. Then she signs the payload with her Megolm session private key and sends it
in an m.room.encrypted message.
When Bob wants to decrypt the message, he first checks the signature of the encrypted payload using Alice’s Megolm session’s public key. Next he finds the ratchet index from the payload and uses the Megolm ratchet to generate bits and passes those bits through HKDF to produce an AES key and IV and a MAC key. He then computes the MAC of the ciphertext using the MAC key and compares it against what Alice sent. Lastly, he decrypts the message using AES.
I hope that you now fully understand the diagram in Figure 6 and understand Megolm in broad strokes. I hope that this article has provided you a good mental model for what Megolm is. I hope that this article will be a starting point for expanding your understanding of cryptography in Matrix. I have intentionally left out discussions about payload formats, byte layout, etc. as they are rather tedious, and already described very well in the Megolm documentation. I highly recommend reading that documentation if you would like to learn more about Megolm.
Cryptography in Matrix is often perceived as scary. I challenge this assertion and believe that Matrix cryptography is not difficult. It is complex, but not difficult. I hope that this article has made a small part of Matrix cryptography (Megolm) not feel scary anymore.
Official Documentation for Megolm is in its README. Its usage within Matrix is described in Section 10.12.4.3
m.megolm.v1.aes-sha2of the Matrix Spec. ↩︎What “CBC” means is not particularly relevant but included for completeness’ sake. ↩︎
The Matrix Spec recommends that Megolm sessions are only used for 100 messages, so this ability to skip values is unnecessary for most cases. Even for the cases that it is useful (Beeper has a very high rotation threshold), it’s probably quite over-engineered. ↩︎
If you want to skip by \(2^8\) for example, you would reset the first part using the rollover method described above, and increment the second part by one. This means that to get to the \(n^{\text{th}}\) ratchet value, you at most have to do 1020 HKDF computations (each of the four parts of the ratchet can be incremented 255 times). ↩︎
