Differential Fuzzing Libolm and Goolm

Background

When we at Beeper started working on the new Android app, based on mautrix-go, we initially tried using goolm as the crypto implementation instead of libolm. We almost immediately ran into issues for unknown reasons, and rather than fighting with cryptography, we decided to just put in the work to get libolm working in the Android app.

However, libolm is annoying for multiple reasons.

1. It’s a C++ library, so in order to use it from Go, you have to use cgo to import the functions. This makes cross-compiling difficult/impossible, and also requires that libolm is installed on the runtime system. A pure Go implementation like goolm compiles everything necessary into the single executable binary.
2. libolm is effectively being deprecated with all new development happening in vodozemac which is a Rust library and probably even more difficult to use from Go than libolm.

I wanted to figure out why we were having these issues by finding the discrepancies between the two implementations, but I wasn’t quite sure how to actually accomplish this goal until Tulir and I were at a talk at FOSDEM about differential fuzzing. Tulir leaned over to me and said, this would be a great way to test libolm and goolm!

📕 Differential fuzzing: a technique which attempts to detect bugs by providing the same input to different implementations of the same application and observing the differences in their execution. (Wikipedia)

Every third Friday, Beeper has a BRAD¹ day which is a day where all employees are encouraged to work on a project that is unrelated to anything on the current roadmap. Many projects are to scratch an itch (creating better tooling, upgrading a library, etc.), to experiment with a new technology, or to try and prove out a new idea. Sometimes, BRAD projects have turned into actual company priorities such as what happened with hungryserv.

Thus, for basically every BRAD day that I have participated in since FOSDEM, I have been working on getting goolm and libolm to a point where they could be differential fuzzed within mautrix-go.

Interface-ifying

The biggest challenge that I faced was that the way we switched between the libolm and goolm implementations was using build flags. Specifying -tags=goolm would compile in the goolm implementation of Olm, while not specifying the tag would compile in the libolm implementation of Olm. Both implementations defined the same methods within the olm package, which provided a unified interface to users of the olm package so the underlying implementations could be switched between without any code changes outside of that package. However, because the build flags determine which code is compiled, the two implementations could not exist at the same time because they defined the same functions.

The solution to this came again from Tulir: interfaces! Both goolm and libolm provide a set of primitives which offer the same basic interface. So I started by interface-ifying the two olm implementations so that we can have libolm and goolm existing in the same codebase and test them against each other. For example, this is the interface for decrypting messages:

// PKDecryption is an interface for decrypting messages.
type PKDecryption interface {
	// PublicKey returns the public key.
	PublicKey() id.Curve25519

	// Decrypt verifies and decrypts the given message.
	Decrypt(ephemeralKey, mac, ciphertext []byte) ([]byte, error)
}

Both the crypto/libolm.PkSigning and crypto/goolm/pk.Decryption structs implement this same interface. The other interfaces are significantly more involved.

What this allows me to do is have both libolm and goolm side-by-side in the codebase not gated by build flags. The user can choose which of the implementations to import, or (most importantly for my use-case) the user can import both at the same time. Once both implementations can be imported, differential fuzzing can be applied.

Differential Fuzzing the Sign Function

The first thing I tried to test was the olm.Account.Sign function which returns the signature of a message using the Ed25519 identity key of the Account.

My test involved creating an account using libolm, exporting it via pickle (the binary representation of the account that we use to persist the account data), importing the pickle into goolm, calling Sign on the same data using the two different implementations, and comparing the outputs. Signatures from Ed25519 are deterministic (there is no random element that is embedded), so I should have received the same signatures, but the signatures from goolm and libolm were different!

Is Pickling Broken?

This is obviously wrong, so the first thing that I looked into was whether our pickling logic was incorrect. I did many experiments involving round-tripping the pickled values through both implementations (generating with libolm, importing into goolm, exporting with goolm, expecting the values to be the same) and all of those tests passed. I tried reversing the generation (generating with goolm instead) and many other round-trip combinations, but none of them failed. Thus, my hypothesis that the pickling was the problem turned out false.

Internally Inconsistent!?

However, during this round-tripping exploration, I decided to add in a test for internal consistency within the goolm side after importing from libolm. I added a test to ensure that the public key derived from the private key was the same as the public key that libolm reported. It turns out, they were different!

assert.Equal(t,
	goolmAccount.IdKeys.Ed25519.PrivateKey.PubKey(),
	goolmAccount.IdKeys.Ed25519.PublicKey) // this assertion failed!

Which means that whatever private key we were getting from libolm didn’t match each other!*

*or so I thought

C Struct Snooping

Both the public and private keys of the Ed25519 keys are both included in the pickle value, so as far as I could tell, the public and private keys that libolm and goolm were using were identical! However, I wanted to double-check by actually inspecting the bytes of the private and public keys.

I was able to verify that both libolm and goolm had the same public key trivially because there are functions in both implementations for retrieving the public key bytes.

However, verifying that the private key bytes were the same was a different story entirely. It is easy to introspect goolm’s internals and get the private keys, but libolm does not expose functions for getting the private key (it only exposes a way to get the pickled value of the entire account). However, libolm does not allocate any memory itself (you have to pass it a byte buffer to put all of its data into), so I could inspect the byte buffer and cross-reference it with the byte layout to see if it matched.

At this point, I figured out that megolm sessions also have Ed25519 keys, and are a lot less heavy than accounts, so I made a reproduction of the issue with megolm sessions and did a memory dump of the libolm megolm session struct. The result? The bytes are equal!

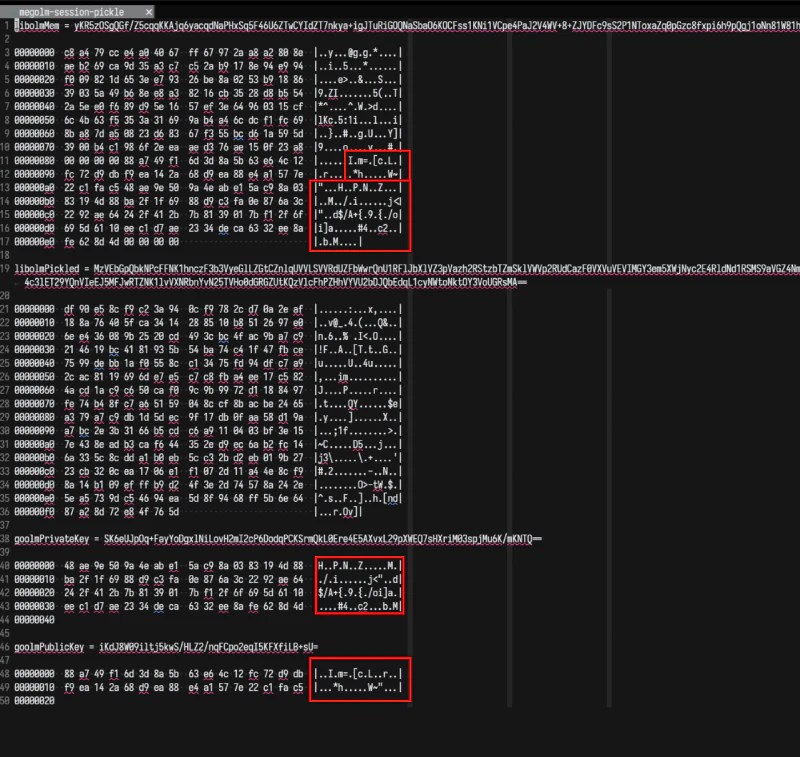
So, at this point I know that the private key bytes being used by libolm and goolm are identical, but the signatures are still turning out different!

Different Ed25519 Binary Format?

Tulir then said something in our chat which led me down a (long) path to solving the mystery. He said:

elliptic curves have those weird encodings where if you encode only one coordinate, then there are two possible keys it can represent. I wonder if it’s somehow related to that

(It turned out to not be exactly that, but it was an encoding issue.)

So, I started looking at different formats that Ed25519 private keys are stored. The Go standard library crypto/ed25519 implementation is very clear about what format it uses. The documentation states (emphasis my own):

Package ed25519 implements the Ed25519 signature algorithm. See https://ed25519.cr.yp.to/.

These functions are also compatible with the “Ed25519” function defined in RFC 8032. However, unlike RFC 8032’s formulation, this package’s private key representation includes a public key suffix to make multiple signing operations with the same key more efficient. This package refers to the RFC 8032 private key as the “seed”.

What this means is that the public key is just the last 32 bytes of the private key.

So, the next step was to figure out if other formats exist, and whether libolm used one of the other formats. I found many different resources, but Brian Warner’s blog post caught my eye because of this diagram:

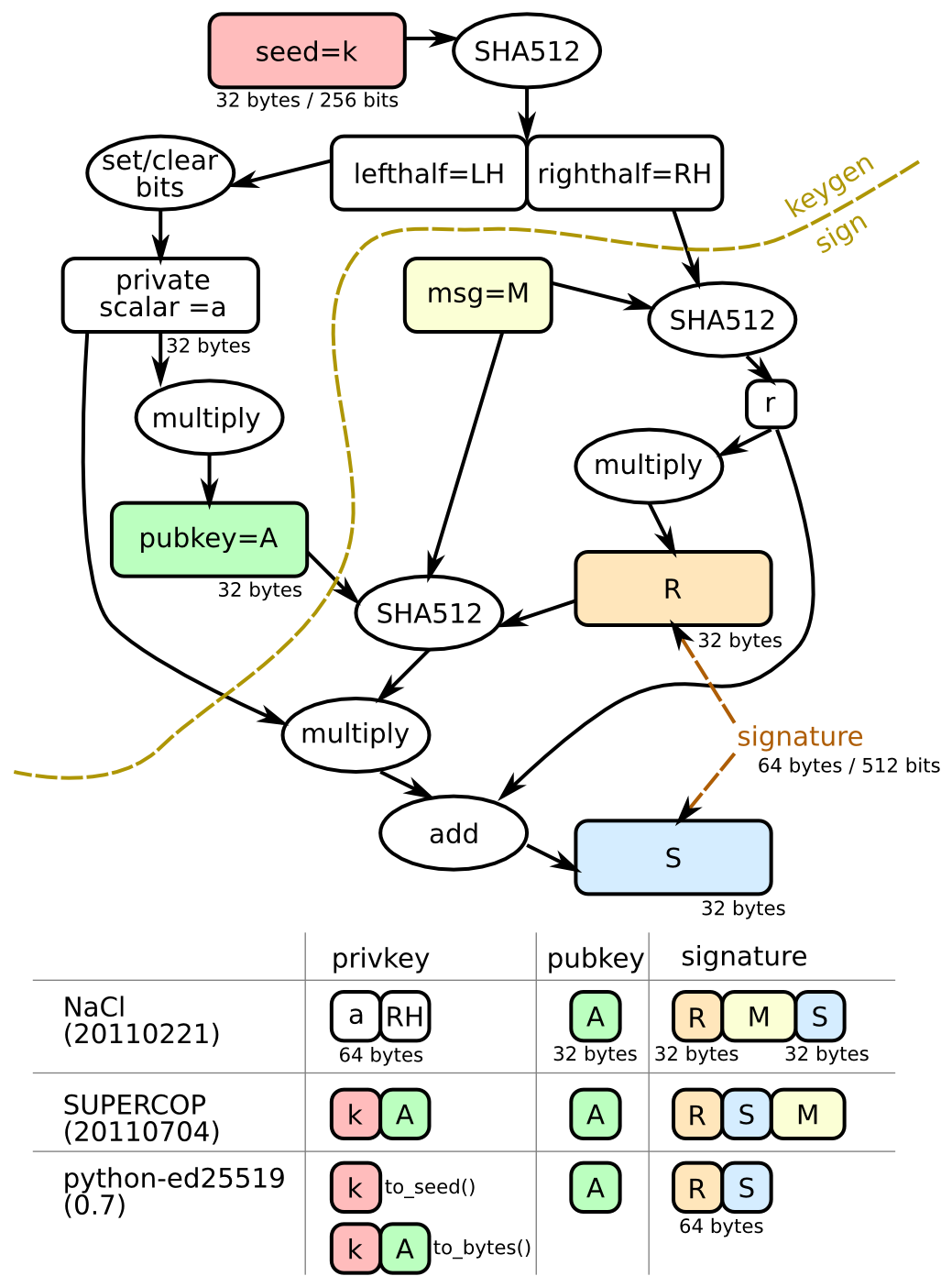
According to the table at the bottom, there are two main ways to store the private key: storing the seed and the public key, or storing the private scalar and the righthalf. Both of these result in 64-bytes, which means that if libolm was using a different representation, it would not be obvious from key size alone, nor would pickling round-tripping tests catch the discrepancy.

According to the libolm readme, the implementation that it uses is based on SUPERCOP, so I expected that it would use the same private key representation, but if it did, it would match what Go expects and I wouldn’t be writing this article.

Epiphany

I asked what format libolm uses in the End-to-end encryption in Matrix room on this past Saturday morning, but (understandably due to it being a weekend) nobody responded to me. So, I decided to do some more digging on Saturday evening and after much DuckDuckGoing and Googling, I found this StackOverflow question and answer which described the exact symptoms I was observing, and provided code for getting from the SHA512 value to a public key. So, I applied that code (I had to make some slight modifications) to one of the libolm private keys that I was testing with, and compared it against the expected public key from libolm, and they matched!

So, what it appears is that libolm actually stores Ed25519 private keys in neither the NaCl format, nor the SUPERCOP format but instead stores the SHA512 result (left and right half).

It turns out that the private and public key exported by libolm do in fact match each other, the private key is just in a different format than the Go crypto/ed25519 package expects.

Our Very Own ed25519 Implementation

It is impossible to reverse a cryptographic hash (of which SHA512 is one). Thus, there is no way to get from the libolm format back to the format required by the Go standard library. Unfortunately, this means that we are going to have to maintain our own implementation of Ed25519 that uses the filippo.io/edwards25519 library directly and stores the private key in the libolm format, rather than taking advantage of the crypto/ed25519 package in the stdlib.

As soon as I switched out the crypto/ed25519 package for a custom package that uses the libolm representation, the account tests started passing, and most of the session tests started passing as well! There’s still one session test that is not working, but I don’t think that it’s related to the private key representation, so that is a mystery for another day!